길고 길었던 알고리즘의 삽질이 끝났다.
사실 슬라이딩 윈도우까지 가진 못했다. 필자의 게으름 + 약속들의 결과물이다. 인정할 건 인정한다.
그래서 오늘은 투 포인터에 대한 내용만 설명하려고 한다.
사실 슬라이딩 윈도우는 문제집에 있는 문제가 몇 개 없어서 단톡방에 있는 분들께 추천을 또 받아서 풀어야 할 것 같기도 하고
(문제가 기하급수적으로 늘어날 수 있다.),
투 포인터는 2가지의 방식이 있기 때문에 알고리즘 유형들만 따로 모아서 정리하려고 이렇게 알고리즘 카테고리를 새로 팠다.
덤으로 누적합에 대한 알고리즘도 이 카테고리에 정리를 한 다음, 문제들을 모아둘 생각이다.
우선 투 포인터에 대한 설명을 하려면 그림으로 보는게 가장 이해가 빠르다.
투 포인터는 총 2가지의 종류로 나뉘는데, start 변수와 end 변수가 둘 다 같은 방향에서 시작하는 경우가 있고,
start 변수와 end 변수가 서로 다른 방향에서 시작하는 경우가 있다. 이를 구별하는 방법은 아주 간단하다.
다음 그림과 같이 연속된 숫자가 저장된 배열이 있다. 배열 내의 연속된 숫자들의 합으로 합이 6인 경우를 찾아보자.
ex) 1+2+3 = 6, 2+3+4=9 등등..
초록색 화살표는 start 변수, 주황색 화살표는 end 변수이다. (둘 다 배열의 인덱스변수다.)

sum은 화살표가 가리키는 값의 누적합이며, 6을 기준으로 start가 올라가고 end가 증가하는 것을 볼 수 있다.
start를 올리는 이유는 누적합에서 sum 값이 지정한 타겟보다 크다면 줄이기 위해서 start를 증가시키는 것이다.
즉, sum의 값을 줄이기 위해 사용된다는 것이다.
그럼 end를 올리는 이유는 무엇일까? start와는 반대로, sum의 값을 증가시키기 위함이다.
따라서 start를 따로 더하거나 그러지 않아도 누적합을 구할 수 있는 것이다.
이번에는 연속되지 않지만 합이 6이 될 수 있는 경우의 수를 구해보자.
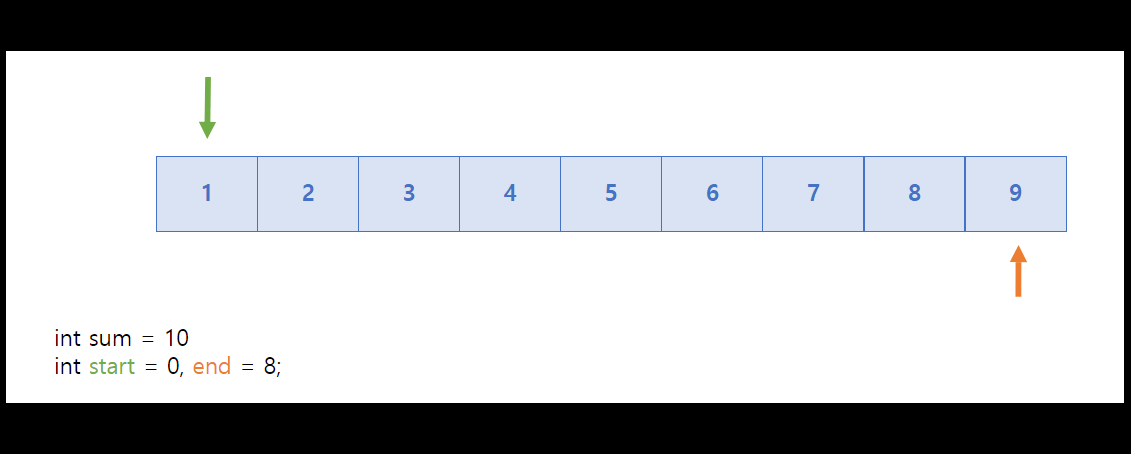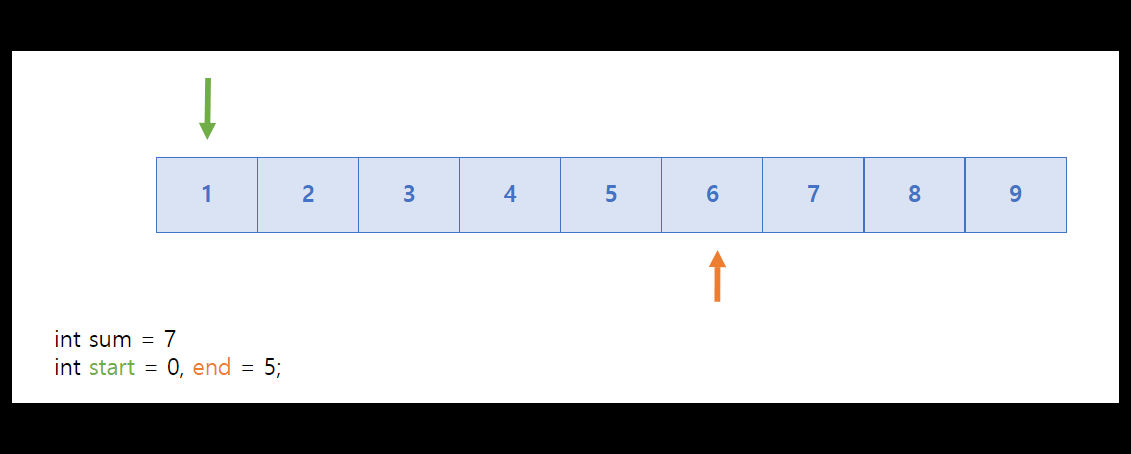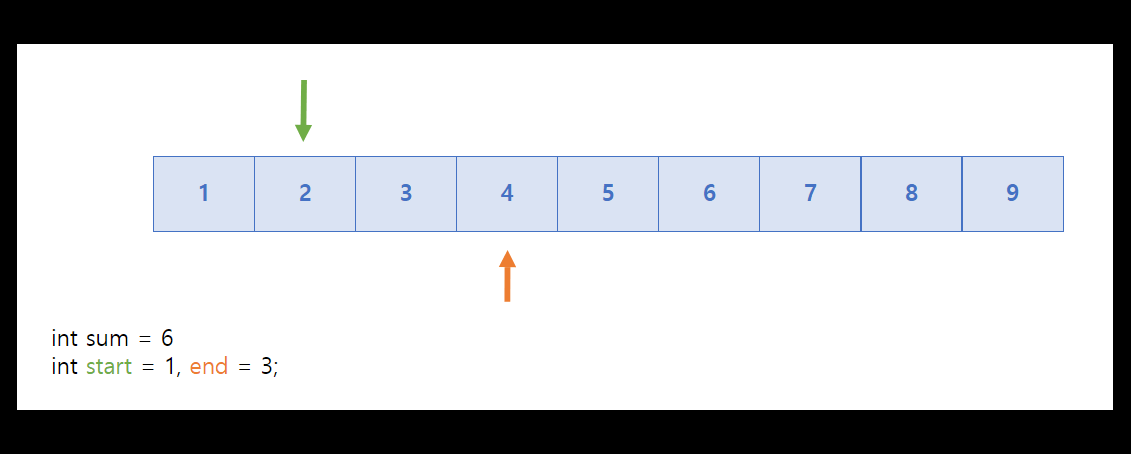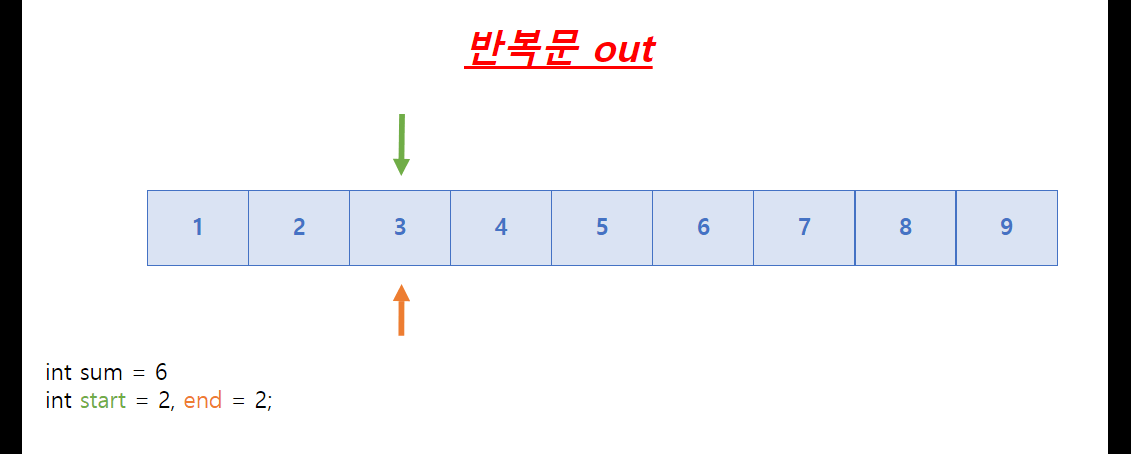
sum은 화살표가 가리키는 값의 합이며, 이는 위에 쓰였던 같은 방향으로 진행되는 투 포인터와 구분되는 가장 핵심되는 포인트이다.
이번에는 위에 쓰인 흐름과는 다르게 start가 sum이 6이 됐을 때 증가한다.
위에 쓰인 start는 sum의 값을 줄이기 위해 사용됐지만, 여기에서 쓰인 start는 다음 경우의 수로 넘어가기 위해서 start를 증가시키는 것이기 때문이다. 또한 end는 점점 9에서 부터 줄어들면서 1과 더해서 6이 나오는 숫자를 찾는다.
이것도 위의 end와 다른 방식이다. 이는 sum의 값이 타겟 값이 되는 경우의 최댓값을 찾기 위해서다.
ex)1+5, 2+4 .. 할 때 5가 최댓값이다.
투포인터는 이렇게 미묘하게 다른 2가지의 방식이 있지만, 제대로 이해하고 넘어가면 흐름 자체는 어렵지 않을
것이다.
다음은 이 개념들을 이해하기 좋은 문제들이다.
이 개념들을 활용하여 풀어보면 충분히 이해하기 쉬울 것이다. (추후 추가 예정)
1. 용액 - https://www.acmicpc.net/problem/2467
2467번: 용액
첫째 줄에는 전체 용액의 수 N이 입력된다. N은 2 이상 100,000 이하의 정수이다. 둘째 줄에는 용액의 특성값을 나타내는 N개의 정수가 빈칸을 사이에 두고 오름차순으로 입력되며, 이 수들은 모두 -
www.acmicpc.net
2. 겹치는 건 싫어 - https://www.acmicpc.net/problem/20922
20922번: 겹치는 건 싫어
홍대병에 걸린 도현이는 겹치는 것을 매우 싫어한다. 특히 수열에서 같은 원소가 여러 개 들어 있는 수열을 싫어한다. 도현이를 위해 같은 원소가 $K$개 이하로 들어 있는 최장 연속 부분 수열
www.acmicpc.net
3. 스터디 그룹 - https://www.acmicpc.net/problem/14572
14572번: 스터디 그룹
첫 줄에 학생의 수 N, 알고리즘의 수 K, 문제에 설명한 D가 주어진다. (1 ≤ N ≤ 105, 1 ≤ K ≤ 30, 0 ≤ D ≤ 109) 이어 N명의 학생에 대한 정보가 아래와 같이 주어진다. M d (0 ≤ M ≤ K, 0 ≤ d ≤ 109): 해
www.acmicpc.net
다음부터는 책에 있던 문제들이다.
1. 수 들의 합 5 - https://www.acmicpc.net/problem/2018
2018번: 수들의 합 5
어떠한 자연수 N은, 몇 개의 연속된 자연수의 합으로 나타낼 수 있다. 당신은 어떤 자연수 N(1 ≤ N ≤ 10,000,000)에 대해서, 이 N을 몇 개의 연속된 자연수의 합으로 나타내는 가지수를 알고 싶어한
www.acmicpc.net
2. 주몽 - https://www.acmicpc.net/problem/1940
1940번: 주몽
첫째 줄에는 재료의 개수 N(1 ≤ N ≤ 15,000)이 주어진다. 그리고 두 번째 줄에는 갑옷을 만드는데 필요한 수 M(1 ≤ M ≤ 10,000,000) 주어진다. 그리고 마지막으로 셋째 줄에는 N개의 재료들이 가진 고
www.acmicpc.net
3. 좋다 - https://www.acmicpc.net/problem/1253
1253번: 좋다
첫째 줄에는 수의 개수 N(1 ≤ N ≤ 2,000), 두 번째 줄에는 i번째 수를 나타내는 Ai가 N개 주어진다. (|Ai| ≤ 1,000,000,000, Ai는 정수)
www.acmicpc.net
다음은 저 문제들을 해결하기 위한 필자의 삽질 과정들이다.
(링크가 되어있지 않은 글은 아직 업로드되지 않았다는 것이므로, 링크가 추가된다면 이용하길 바란다.)
1. 용액 (2022.09.19 작성 완료)
2. 겹치는 건 싫어
3. 수 들의 합 5 (2022.09.19 작성 완료)
4. 주몽 (2022.09.20 작성 완료)
5. 좋다 (2022.09.20 작성 완료)
6. 스터디 그룹 (2022.09.23 추가)